July 12, 2018
Hey Developer,
I am bringing you another high quality Java solution. This time, I am solving the Max Double Slice Sum problem which can be found here.
My solution has a runtime of O(N) and space complexity of O(N). I think this problem is conceptually difficult to think about, however I will do my best to explain it.
Explanation:
Let’s look at the picture below and make some key observations.
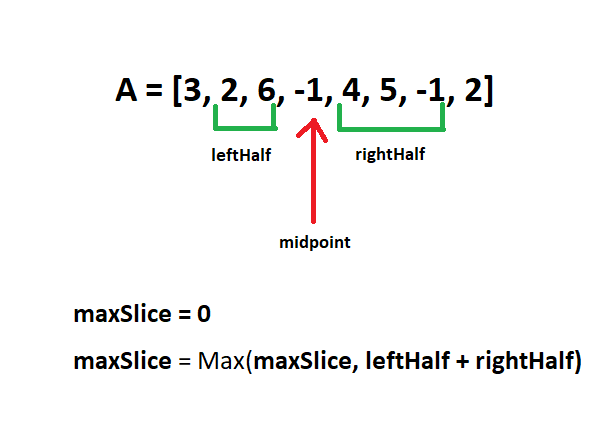
After digesting the equation for the problem, The sum of double slice (X, Y, Z) is the total of A[X + 1] + A[X + 2] + … + A[Y − 1] + A[Y + 1] + A[Y + 2] + … + A[Z − 1], we can simply see that the problem can be separated into two subarrays. The minimum value for our slice is always 0, because consecutive numbers such as (2,3,4) will yield 0 + 0 = 0.
The first subarray called leftHalf is from [1, Y).
The second subarray called rightHalf is from (Y, N – 1].
To solve the problem, we maximize the left slice, then we maximize the right slice and combine them. In the example above the maximized left slice is 2 + 6 = 8, and the maximized right slice is 4 + 5 = 9. This gives us 8 + 9 = 17.
Now of course, we know this is the correct answer by the problem description, but in reality we are checking the max double slice for Y between [1,N-1].
The code below works like this:
NOTE: The tricky part is figuring out which value in our array goes with our current rightHalf.
Below is the code for my Java solution.
class Solution { public int solution(int[] A) { // number of elements in A int N = A.length; // variable representing the maximum slice int maxSlice = 0; // holds the results for the left half calculations int [] leftHalfResults = new int [N]; // used for calculation of the right half int rightHalf = 0; // maximum slice of the first half // starts at 1, because our value at index 0 is always going to be 0 // ends at N-2, because that is the maximum size for our left half // leftHalfResults[0] = 0; for (int k = 1; k < N-2; k++) { leftHalfResults[k] = Math.max(0, leftHalfResults[k-1] + A[k]); } // calculate the maximum right half // At the same time calculate the maximum slice for the current leftHalf and rightHalf combination for (int i = N-1; i > 1 ; i--) { // the tricky part was to figure out what k should be to make sure the two halves correspond to the same midpoint // this took some time to do using System.out.println() int k = i-2; // when the right half is 0 if (i == N-1) { rightHalf = 0; maxSlice = Math.max(maxSlice, leftHalfResults[k] + rightHalf); } else { rightHalf = Math.max(0, rightHalf + A[i]); maxSlice = Math.max(maxSlice, leftHalfResults[k] + rightHalf); } } return maxSlice; } }
Comments
Hello Bogdan,
You are an amazing coder. I have been looking for this JavaScript solution for some time now and this is it!