Java Solution to Codility’s Max Double Slice Sum Problem

July 12, 2018

Hey Developer,

I am bringing you another high quality Java solution. This time, I am solving the Max Double Slice Sum problem which can be found here.

My solution has a runtime of O(N) and space complexity of O(N). I think this problem is conceptually difficult to think about, however I will do my best to explain it.

Explanation:

Let’s look at the picture below and make some key observations.

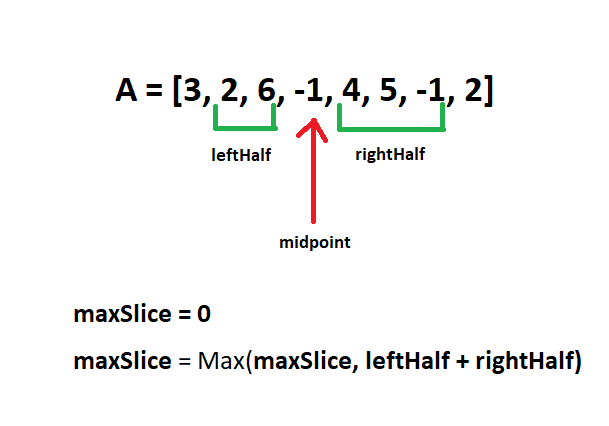
After digesting the equation for the problem, The sum of double slice (X, Y, Z) is the total of A[X + 1] + A[X + 2] + … + A[Y − 1] + A[Y + 1] + A[Y + 2] + … + A[Z − 1], we can simply see that the problem can be separated into two subarrays. The minimum value for our slice is always 0, because consecutive numbers such as (2,3,4) will yield 0 + 0 = 0.

The first subarray called leftHalf is from [1, Y).

The second subarray called rightHalf is from (Y, N – 1].

To solve the problem, we maximize the left slice, then we maximize the right slice and combine them. In the example above the maximized left slice is 2 + 6 = 8, and the maximized right slice is 4 + 5 = 9. This gives us 8 + 9 = 17.

Now of course, we know this is the correct answer by the problem description, but in reality we are checking the max double slice for Y between [1,N-1].

The code below works like this:

1. Go through array A and store the maximized leftHalf into an array for later use.
2. Go through array A and calculate the maximized rightHalf
3. As soon as rightHalf is calculated we can use it in combination with the previously stored leftHalf result to calculate our maxSlice

NOTE: The tricky part is figuring out which value in our array goes with our current rightHalf.

Below is the code for my Java solution.

class Solution {
	public int solution(int[] A) {
		// number of elements in A
		int N = A.length;
		// variable representing the maximum slice
		int maxSlice = 0;	
		// holds the results for the left half calculations
		int [] leftHalfResults = new int [N];
		// used for calculation of the right half
		int rightHalf = 0;
 
		// maximum slice of the first half
		// starts at 1, because our value at index 0 is always going to be 0
		// ends at N-2, because that is the maximum size for our left half
		// leftHalfResults[0] = 0;
		for (int k = 1; k < N-2; k++) {
			leftHalfResults[k] = Math.max(0, leftHalfResults[k-1] + A[k]);
		}
 
 
		// calculate the maximum right half 
		// At the same time calculate the maximum slice for the current leftHalf and rightHalf combination
		for (int i = N-1; i > 1 ; i--) {
			// the tricky part was to figure out what k should be to make sure the two halves correspond to the same midpoint
			// this took some time to do using System.out.println()
			int k = i-2;
			// when the right half is 0
			if (i == N-1) {
				rightHalf = 0;
				maxSlice = Math.max(maxSlice, leftHalfResults[k] + rightHalf);
			}
			else {
				rightHalf = Math.max(0, rightHalf + A[i]);
				maxSlice = Math.max(maxSlice, leftHalfResults[k] + rightHalf);
			}
		}
 
        return maxSlice;
	}
}